1.State Varignons Theorem
The algebraic sum of the moments of any number of forces about any point in their plane is equal to the moment of their resultant about the same point .Varignons theorem is also known as theorem of movements
2.Give the equations of equilibrium of coplanar force systems
Equilibrium Equation For Coplanar force system:
For a force system which comprises of forces with their lines of action in the same plane and the moments due to couples which are directed perpendicular to the plane, the conditions of equilibrium can be written as:
Σ Fx = 0 (sum of all horizontal forces)
Σ Fy = 0 (sum of all verfical forces)
and Σ M = 0 (sum of all moments)
the summation of moments may be taken about any point on the XY plane but it should be about the Z-axis through the chosen point. The body thus can only be in equilibrium if the algebraic sum of all the external forces and their moments about any point in their plane is zero.
3.State Principles of Transimissibility?
The principle of transmissibility says that a force can be applied
anywhere along its line of action, with no change in any of the
effects on the body.
4.State Lami's Theorem?
Simple:
When three forces act on a particle in equilibrium, the magnitude of each is proportional to the sine of the angle between the other two.
Elaborated:
In statics, the Lami's theorem is an equation relating the magnitudes of three coplanar, concurrent and non-collinear forces, which keeps an object in static equilibrium, with the angles directly opposite to the corresponding forces. According to the law,
where A, B and C are the magnitudes of three coplanar, concurrent and non-collinear forces, which keeps the object in static equilibrium, and
α, β and γ are the angles directly opposite to the forces A, B and C respectively.
5.Define Moment of a Force
The Moment of a force is a measure of its tendency to cause a body to rotate about a specific point or axis. This is different from the tendency for a body to move, or translate, in the direction of the force. In order for a moment to develop, the force must act upon the body in such a manner that the body would begin to twist. This occurs every time a force is applied so that it does not pass through the centroid of the body. A moment is due to a force not having an equal and opposite force directly along it's line of action.
6.Centroid
the word centroid means the geometric center of the object's shape, as above, but barycenter may also mean its physical center of mass or the center of gravity, depending on the context. Informally, the center of mass (and center of gravity in a uniform gravitational field) is the average of all points, weighted by the local density or specific weight. If a physical object has uniform density, then its center of mass is the same as the centroid of its shape.
7.Centre of Gravity
The center-of-gravity (CG) is the point at which an aircraft would balance if it were possible to suspend it at that point. It is the mass center of the aircraft, or the theoretical point at which the entire weight of the aircraft is assumed to be concentrated.[1] Its distance from the reference datum is determined by dividing the total moment by the total weight of the aircraft.[2] The center-of-gravity point affects the stability of the aircraft. To ensure the aircraft is safe to fly, the center-of-gravity must fall within specified limits established by the manufacturer.
8.Parallel Axis Theorem
The moment of inertia of any object about an axis through its center of mass is the minimum moment of inertia for an axis in that direction in space. The moment of inertia about any axis parallel to that axis through the center of mass is given by
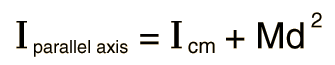
The expression added to the center of mass moment of inertia will be recognized as the moment of inertia of a point mass - the moment of inertia about a parallel axis is the center of mass moment plus the moment of inertia of the entire object treated as a point mass at the center of mass.
9.Kinematics
It is the study of a body in motion,with considering the forces,that cause motion.
Kinematics is used to relate displacement,velocity,acceleration,time taken etc.. of bodies without any reference to the cause of motion.
10.Static friction
Static friction is friction between two solid objects that are not moving relative to each other. For example, static friction can prevent an object from sliding down a sloped surface. The coefficient of static friction, typically denoted as μs, is usually higher than the coefficient of kinetic friction.
The static friction force must be overcome by an applied force before an object can move. The maximum possible friction force between two surfaces before sliding begins is the product of the coefficient of static friction and the normal force: f = \mu_s F_{n}\,. When there is no sliding occurring, the friction force can have any value from zero up to F_{max}\,. Any force smaller than F_{max}\, attempting to slide one surface over the other is opposed by a frictional force of equal magnitude and opposite direction. Any force larger than F_{max}\, overcomes the force of static friction and causes sliding to occur. The instant sliding occurs, static friction is no longer applicable—the friction between the two surfaces is then called kinetic friction.
11.Kinetic Friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground). The coefficient of kinetic friction is typically denoted as μk, and is usually less than the coefficient of static friction for the same materials.[13][14] In fact, Richard Feynman reports that "with dry metals it is very hard to show any difference."[15] Finally, new models are beginning to show how kinetic friction can be greater than static friction.

No comments:
Post a Comment